la fuerza es una magnitud vectorial que mide la razón de cambio de momento lineal entre dos partículas o sistemas de partículas. Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los materiales. No debe confundirse con los conceptos de esfuerzo o de energía.
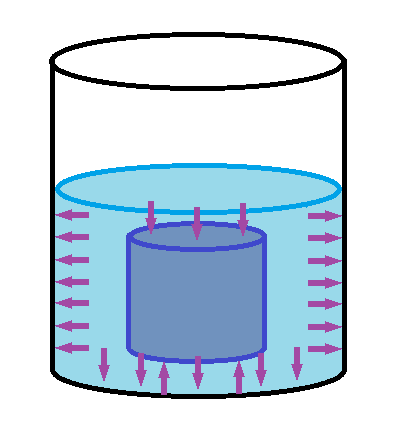
La hidrostática es la rama de la mecánica de fluidos o de la hidráulica que estudia los fluidos en estado de equilibrio; es decir, sin que existan fuerzas que alteren su movimiento o posición. Los principales teoremas que respaldan el estudio de la hidrostática son el principio de Pascal y el principio de Arquímedes.
Aunque los fluidos obedecen a las mismas leyes físicas que los sólidos, la facilidad con la que cambian de forma hace que sea conveniente estudiar pequeñas porciones en un lugar de todo el fluido. Por eso se reemplazan las magnitudes extensivas (que dependen de la cantidad de materia) por las magnitudes intensivas (que dependen de la cantidad de materia) la masa se reemplaza por la densidad y el peso se reemplazara por el peso especifico
PRESIÓN
La presión (P) se relaciona con la fuerza (F) y el área o superficie (A) de la siguiente forma: P=F/A.
La ecuación básica de la hidrostática es la siguiente:
dP = ρgdh
Siendo:
P: presión
ρ: densidad del fluido
g: la aceleración gravitatoria de la Tierra
h: altura
PRESIÓN HIDROSTATICA

La presión hidrostática, por lo tanto, da cuenta de la presión o fuerza que el peso de un fluido en reposo puede llegar a provocar. Se trata de la presión que experimenta un elemento por el sólo hecho de estar sumergido en un líquido.
La presión hidrostática (p) puede ser calculada a partir de la multiplicación de la gravedad (g), la densidad (d) del líquido y la profundidad (h). En ecuación: p = d x g x h
EJEMPLO
Ejercicio 1
¿Cuál es la presión que soporta un buzo sumergido a 10 metros de profundidad en el mar?
Datos: Densidad del agua de mar = 1,025 kg/L. Presión atmosférica 101325 Pa.
Datos: Densidad del agua de mar = 1,025 kg/L. Presión atmosférica 101325 Pa.
Solución
Primero convertimos las unidades dadas en el ejercicio a unidades del Sistema Internacional:
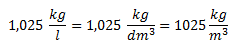
Luego aplicamos la definición de presión hidrostática, considerando la presión atmosférica.
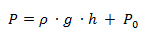
Reemplazamos los valores del ejercicio en la fórmula:
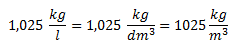
Luego aplicamos la definición de presión hidrostática, considerando la presión atmosférica.
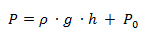
Reemplazamos los valores del ejercicio en la fórmula:
EJEMPLO 2
Ejercicio 4
Determinar la fuerza que equilibra el sistema, sabiendo que las superficies s1 y s2 tienen diámetros circulares de 10 y 40 cm respectivamente.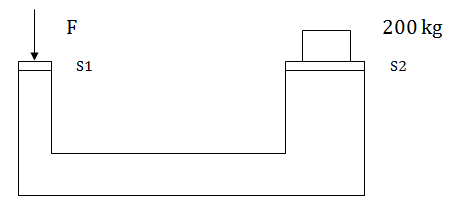
Solución
Convertimos los valores dados a las unidades básicas del SI y calculamos los radios: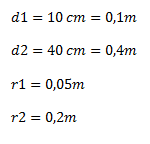
Calculamos las superficies s1 y s2 en función de los radios:
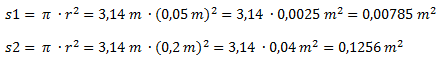
Calculamos la fuerza que ejerce la masa en s2. Para eso utilizamos la fórmula de peso.
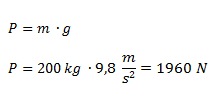
Planteamos la ecuación de la prensa hidráulica reemplazando a la fuerza 1 por F y a la fuerza 2 por el peso.
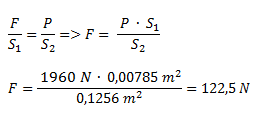
PARA MAS DUDA CONSULTAR EL VIDEO
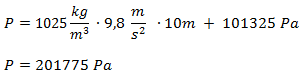
No hay comentarios.:
Publicar un comentario